Unisci i punti adiacenti con trattini orizzontali o verticali così da tracciare un “circuito chiuso” (o anche Slitherlink) senza incroci o diramazioni, che rispetti le seguenti regole:
- Ciascuna cifra indica da quanti trattini è circondata;
- Dove non ci sono cifre sta a voi stabilire il numero di trattini (da 0 a 3) da tracciare.
INIZIARE DAI 3
La prima cosa di cui dobbiamo occuparci è di individuare le certezze: i trattini sicuramente presenti e i lati delle caselle che sicuramente non possono far parte del circuito. Valutiamo le situazioni che possiamo incontrare, iniziando da quelle più comuni. Consideriamo quindi le caselle contenenti il numero 3.
 INIZIARE DAGLI ANGOLI
INIZIARE DAGLI ANGOLI
Un altro metodo di partenza consiste nel valutare la situazione negli angoli.
La prima cosa di cui dobbiamo occuparci è di individuare le certezze: i trattini sicuramente presenti e i lati delle caselle che sicuramente non possono far parte del circuito. Valutiamo le situazioni che possiamo incontrare, iniziando da quelle più comuni. Consideriamo quindi le caselle contenenti il numero 3.
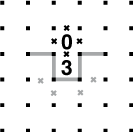
La presenza dei numeri 3 e 0 in due caselle adiacenti offre un metodo di partenza molto valido, perché c’è una sola combinazione possibile. Le x intorno allo 0, infatti, ci aiutano a escludere un lato della casella contenente il 3. I tratti del circuito che circondano il 3 sono ora obbligati, come lo sono anche i due che si estendono ai due lati della casella.

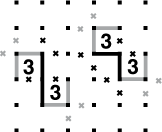
La figura mostra i possibili percorsi dei circuito, quando si trovano due 3 in diagonale. Due dei tre tratti che li circondano sono comuni a tutti i percorsi e possono essere inseriti, così come le “x”.

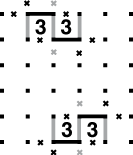
Osserviamo infine i possibili percorsi del circuito, quando i 3 si trovano in caselle adiacenti. Inseriamo i tratti in grigio, in quanto comuni ai due percorsi. Le “x” mostrano l’impossibilità per il circuito di proseguire in quelle direzioni, perché si verrebbero a creare delle diramazioni.

Un altro metodo di partenza consiste nel valutare la situazione negli angoli.
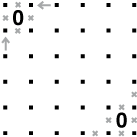
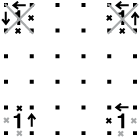
I lati di una casella contenente uno 0 non possono mai essere formati da tratti del Circuito. Se poi, lo 0 si trova in un angolo, ci sono due tratti ulteriori che non possono essere inseriti. Guardando i tratti segnalati dalle frecce possiamo notare che, se questi fossero parte del circuito, finirebbero in un vicolo cieco, un punto, cioé, che non permette di proseguire. Questi due tratti sono da eliminare con delle “x”.

Nel caso degli 1 consideriamo che un tratto, toccato l’angolo dello schema, deve obbligatoriamente proseguire ad angolo retto. L’1 nell’angolo sarebbe in questo caso circondato da 2 tratti, e questo va contro le regole del gioco. Ne consegue che in nessun caso, se nell’angolo è presente un 1, il tratto può toccare l’angolo dello schema. I due lati corrispondenti devono essere bloccati con delle “x”.

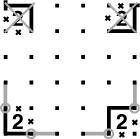
Quando un 2 si trova in un angolo, come mostrato in figura, il circuito può seguire 2 possibili percorsi, senza violare le regole. In ognuna delle 2 situazioni, il percorso passa sicuramente per i due punti cerchiati e prosegue per i due tratti grigi i quali, quindi, fanno sicuramente parte del circuito.

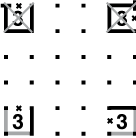
Nel caso dei 3, dei possibili percorsi mostrati in figura, soltanto due sono validi, perché rispettano le regole del gioco. I tratti in comune di questi due percorsi (in grigio) fanno sempre sicuramente parte del circuito e possono essere inseriti da subito.

